Transformations

Or: Is this the kind of problem where you can have more than one answer?

There are a select few topics in algebra that can get me tied up in knots. One of those is function transformations--you know, horizontal & vertical shifts, vertical stretches & compressions, and horizontal & vertical reflections--specifically, those that involve a multiple transformations.

Here's the task I got hung up on the other day:

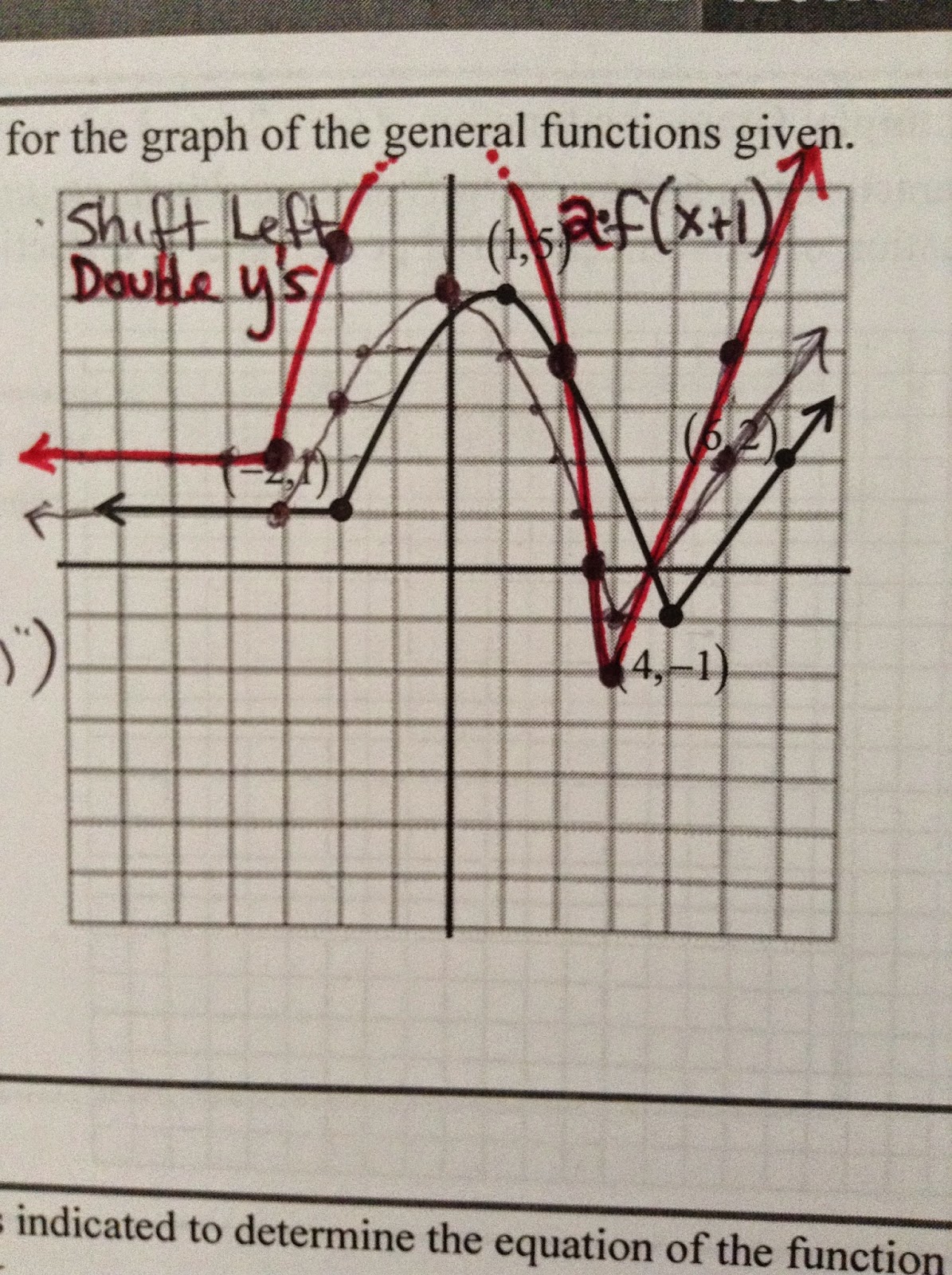
The graph of a function f is shown. Sketch the graph of y = 2f(x+1) - 3.

On these types of tasks, it's not the transformations themselves that get me. There are three transformations at work here, and I can describe them easily enough:

1. Horizontal shift one unit left (because of the x+1).
2. Vertical shift three units down (because of the -3).
3. Vertical stretch by a factor of 2 (basically, double the y-values). 

The part that gets me hung up, at least when I have not done these kinds of problems in a while, is... in which order should I apply the transformations?

Because it makes a big difference! To illustrate, let's trace where the point (-2,1) ends up if we shift-then-double vs. double-then-shift:

• Shift-then-double: (-2,1) --left1--> (-3,1) --down3--> (-3,-2) --double y--> (-3,-4).
• Double-then-shift: (-2,1) --double y--> (-2,2) --left1--> (-3,2) --down3--> (-3,-1).

See? (-3,4) and (-3,-1).. we end up in two different spots.

This is not "the kind of problem you can have two different answers to" (Cathy Humphreys; clipped from one of the videos in this book).

Of course, after thinking it through, it becomes clear that we must mirror the order in which the function 2f(x+1) - 3 is evaluated. If we try to do the transformation in the wrong order, we get stuck in conversations like:

Me: I'm going to subtract 3 first.
You: Subtract 3 from what?
Me: From 2f(x+1). 
You: But you we haven't calculated that yet.
Me: Oh.

The only sequence of transformations that can work is the one that traces the operations involved from input to output. That is, we must:

1. Evaluate (x+1),
2. Apply f,
3. Double the result, and finally
4. Subtract 3.

So to evaluate 2f(x+1) - 3for any particular value of x, we must first calculate f(x+1). The horizontal shift happens first.

f(x+1)

Once we have f(x+1), we double it: 2f(x+1). So the vertical stretch comes second.

2f(x+1)

And once we have 2f(x+1), we can perform the final transformation: subtract 3.

2f(x+1)- 3

Whew. Maybe now that I've written it down, I will be able to remember how to handle problems like these next time without having to walk myself through it again.

Until then... "Mathbots, roll out!"